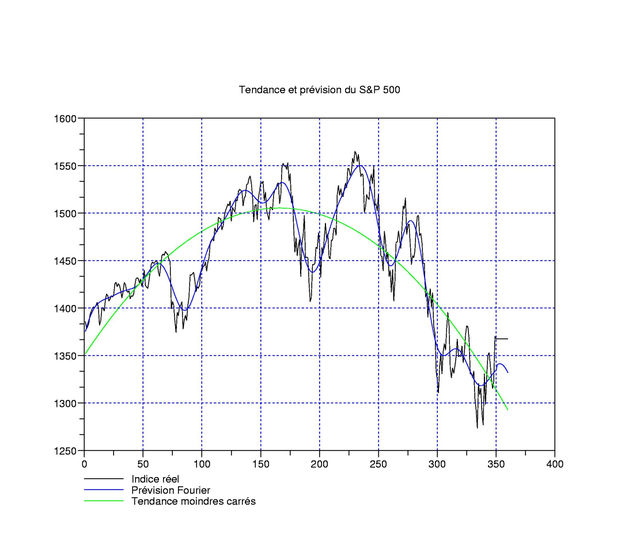
Avez-vous remarqué le changement de 2007 à 2008 ? L’an passé, chaque discours de Bernanke faisait grimper le Dow, cette année, c’est le contraire … Franchement, je suis méchant avec ce pauvre gars, rapport au fait que je n’aimerais pas avoir ses responsabilités par les temps qui courent. Par contre, coté indices, on fait beaucoup de gorges chaudes sur la hausse de ces jours-ci: du coup, voici quelques graphiques sortis de ma petite toolbox personnelle. Ce soir, pas de tendances affines par morceaux comme hier, mais au contraire, on regarde ce qui se passe lorsque l’on cherche des tendances polynomiales (donc infiniment régulières) et que l’on les extrapole très légèrement avec les fluctuations restantes traitées en Fourier avec 10 modes seulement. Le S&P 500 (à gauche) est bien approché par une parabole concave (en vert) sur 350 jours, et le rebond actuel n’a pas l’air d’etre destiné à survivre très longtemps.
Coté Europe, notre CAC national est lui aussi bien par le meme type de tendance parabolique. Le pic actuel n’a pas l’air d’etre en mesure d’affecter sensiblement l’évolution de l’indice, exactement comme le pic passé fin février 2008. On voit bien que la courbe bleue, obtenue en faisant la somme de la tendance verte et des fluctuations filtrées en Fourier passe allègrement à travers. Cela semble suggérer que la dégringolade risque de repartir sous peu, mais elle partira probablement des 4800 points et sera plus lente que celle de mars 2008. La glissade maousse pourrait bien survenir en mai (sell in may and go away) …
Coté DAX, le problème est un peu plus délicat car une parabole ne réalise pas une bonne approximation, il faut passer à une tendance de degré 3 pour bien « attrapper » la forte chute de 2008 (l’indice ayant continué à progresser en 2007, il est « en retard » dans la phase corrective). Pour ce qui touche au rebond actuel, meme verdict, il ne semble pas qu’il doive durer … Toutefois, la tendance baissière étant très abrupte sur cet indice, on pourrait bien avoir un changement à ce niveau-là pour revenir à une parabole comme pour le CAC et le S&P. En quelque sorte, il s’agirait alors de « corriger » un exces baissier.
Justement, cette dernière figure montre l’indice allemand sur la meme période, mais approché par une tendance d’ordre 2 seulement. On voit que celle-ci est « moins belle » puisqu’elle est symétrique alors que l’indice ne l’est pas. Par contre, les fluctuations « voient » bien le rebond actuel. Ceci penche en faveur de l’idée d’un adoucissement de la baisse sur l’indice allemand et de la poursuite de celle-ci sur le CAC et le S&P … Le futur nous le dira!
Je ne comprends pas à quoi cela sert de faire ces régressions polynomiales sur les cours passés… Vous en tirez une analyse quelconque ? Pouvez-vous me l’expliquer ?
Ben, c’est plutot évident! C’est comme faire des moyennes mobiles, mais avec en plus un critère d’optimalité puisque ces régressions sont solutions d’une minimisation convexe.
Oui, j’ai bien compris comment vous obtenez ces régresssions, mais ce n’est pas ma question.
Les MM peuvent être utilisées pour définir des supports en analyse technique. Quid de ce que vous faites ?
Le but du jeu n’est pas d’obtenir des supports/resistances; l’idée est plus de faire la synthèse des évolutions passées sur une certaine fenètre d’observation, de les décomposer entre tendance/fluctuation/bruit et d’extrapoler les 2 premiers morceaux obtenus.
Dans ce post, la tendance est recherchée dans l’espace des polynomes (mais ce n’est pas l’unique espace ou chercher) et la fluctuation sous forme d’harmoniques (meme remarque). Le bruit est identifié en regardant l’autocorrélation de ce qui reste.
L’idée est donc de chercher des possibilités pour l’évolution future de l’indice qui soient en accord avec un passé plus ou moins lointain (plus, c’est mieux) et qui ne contiennent qu’un niveau prescrit de complexité (ici, 10 modes de Fourier et pas plus). Pas grand-chose à voir avec l’AT, donc …
Tres interessant comme approche.
Par contre, les techniques employees, comme la transformee de Fourrier necessite de respecter un certain nombre d’hypotheses (je sais plus lesquelles, tout cela remonte a loin 🙂 :)).
Je suppose que la nature de l’evolution du prix de l’action ne respecte pas ces hypotheses. Donc comment, approcher ou se rapprocher des conditions d’utilision de la transformee de Fourrier par exemple ?
Ou bien on assume le fait que l’on respecte les hypotheses de depart, et on verifie a posteriori ?
Bref, quel(s) element(s) fait que l’application de ces methodes est appropriee ?
Desole pour mon langage non mathematique, tout cela remonte a tres tres loin 🙂 🙂
Zigomar: sur les hypotheses, on a besoin d’un signal dans L1(R) ou L2(R). Ca suffit a pouvoir appliquer la TdF. Maintenant, comme la tendance est obtenue à l’aide d’une minimisation sur l’espace des polynomes, la fluctuation (=l’indice – la tendance) a plusieurs moments nuls, ce qui garantit que le signal a analyser est soit très oscillant, soit décroissant à l’infini.
D’un point de vue numerique, avec la FFT on ne sait rien faire d’autre que périodiser l’échantillon: on doit donc trouver un moyen d’étendre le spectre. Il y a des méthodes pour cela, développées à partir des années 80, jusqu’aux travaux très récents du « compressed sensing ».
Pour reprendre ton exemple, il se trouve que le cours des indices (pas des actions individuelles) est dominé par un nombre restreint de modes de Fourier (moins de 10), et ceci avec une très bonne précision. L’inconvénient est que des mesures journalières nous donnent une résolution de l’ordre de la semaine (toujours le vieux problème de l’échantillonnage).
Ok Laurent, merci pour ces explications.
Fourrier s’applique aux signaux periodiques.
Donc tu periodises ton signale grace a certaines methode avant de proceder a l’analyse.
Je saisis mieux les bases de ton travail.
Ce que je trouve fascinant, c’est que sur les indices, comme tu le soulignes, le resultat de la FFT ne donne pas un signal noyé dans le bruit, et que l’on identifie tres bien les harmoniques principaux.
Faudra que je trouve le temps de potasser ce sujet, cela eveille ma curiosite.
A+
Je ne périodise pas le signal moi-meme, mais du moment que je fais la FFT, celui-ci est périodisé … On ne sait pas calculer numériquement la TdF sans périodiser. Ceci complique un peu les choses, car si on prend le spectre numérique pour argent comptant et que l’on extrapole, on se contente en fait de recoller à droite la fluctuation qui existe sur le bord gauche de l’intervalle des mesures.
Donc il faut faire autre-chose, c’est-a-dire extrapoler le spectre. Pour cela, il faut une « matrice de décimation », en anglais « sparsing matrix » dont le but est de bien compresser le signal. En gros, on cherche une base dans laquelle les « coordonnées » du signal sont presque toutes nulles. Et ceci, tu le fais avec la FFT, ou les ondelettes ou autre chose. C’est à ce niveau que le bruit est séparé, et à l’expérience, c’est assez facile, du moins pour des périodes d’observation suffisamment longues (si tu regardes sur 150 jours ou moins, le bruit devient difficile à filtrer).